D/A コンバータの実際
デジタルに於けるオーディオの問題点と技術的目標として、可聴帯域以上への伸張や24ビット・32ビットとビット数を上げるのは、諧調性や高密度の再現というよりも、実際はローレベルの再現性・量子化ノイズとの戦いである事が、本当の技術的目標であった事が解る。
それは、TDA-1540に始まり TDA-1541 TDA-1547 そして現在の最新鋭のD/Aコンバータに到るまで、同じ軌道の上にある。この問題にどの様に対処したのか、その実際を見てみたい。
試聴記は後日の予定であったのだけれども、結論から先に書いてしまうと、バランス-バランス接続したStuder D-730は凄く良かった。A-730も良いが、音楽を楽しませる表現力は互角で、まったく遜色ない。オーディオ的なニュアンスの豊かさと迫真性では、A-730を凌いでいるようにも聴こえた。A-730は音色がきちんと整えられ、喩えればマスターテープのような音で、D-730はマイクを介した生演奏の音のように感じる。ところが、世間の評価では、圧倒的に【マルチビット】が高く、ワンビットは高域がメロー・低域に力が無いと評される事が多い。確かに単体での音はその傾向があるのかも知れない。
世評の違いは、デジタル変換そのものに依拠している性質なのかを知りたいと思い、詳しく調べる事にした。ところが、基幹の技術であるΔΣ変調が難物で、理解の前に立ち塞がってくる。
当初TDA1547は、開発経緯からコストダウンのための開発と思っていたので、ワンビットだからと、高を括っていた。ところが実際は、TDA1541のブレークスルーを計ったコンバーターであり、その要がΔΣ変調であった。マルチビットからシングル・ビットへの移行は想像以上に大胆である。少し長くなってしまったのだけれども、お付き合い頂ければ有難い。

- Wikipediaより -
【SACD】
デジタルに於けるオーディオの問題点と技術的目標として、可聴帯域以上への伸張や24ビット・32ビットとビット数を上げるのは、諧調性や高密度の再現というよりも、実際はローレベルの再現性・量子化ノイズとの戦いである事が、本当の技術的目標であった事が解る。
それは、TDA-1540に始まり TDA-1541 TDA-1547 そして現在の最新鋭のD/Aコンバータに到るまで、同じ軌道の上にある。この問題にどの様に対処したのか、その実際を見てみたい。
試聴記は後日の予定であったのだけれども、結論から先に書いてしまうと、バランス-バランス接続したStuder D-730は凄く良かった。A-730も良いが、音楽を楽しませる表現力は互角で、まったく遜色ない。オーディオ的なニュアンスの豊かさと迫真性では、A-730を凌いでいるようにも聴こえた。A-730は音色がきちんと整えられ、喩えればマスターテープのような音で、D-730はマイクを介した生演奏の音のように感じる。ところが、世間の評価では、圧倒的に【マルチビット】が高く、ワンビットは高域がメロー・低域に力が無いと評される事が多い。確かに単体での音はその傾向があるのかも知れない。
世評の違いは、デジタル変換そのものに依拠している性質なのかを知りたいと思い、詳しく調べる事にした。ところが、基幹の技術であるΔΣ変調が難物で、理解の前に立ち塞がってくる。
当初TDA1547は、開発経緯からコストダウンのための開発と思っていたので、ワンビットだからと、高を括っていた。ところが実際は、TDA1541のブレークスルーを計ったコンバーターであり、その要がΔΣ変調であった。マルチビットからシングル・ビットへの移行は想像以上に大胆である。少し長くなってしまったのだけれども、お付き合い頂ければ有難い。
D/A コンバータの現在
現在標準的なCD規格の上位規格として、SACD DSDがある。これらも併せて見る事により、今日のD/Aコンバータの位置づけ、そしてTDA1547をより明確にする事になると思う。
----------------------------------------------------------------------------------------------------------------------【SACD】
オーディオデータはCD-DAやDVDビデオで利用されているリニアPCMと称される16bit44.1kHzではなく、ΔΣ変調を併用した高速標本化低bitである1bit2.8224MHz(=2822.4kHz)である。この量子化語長・標本化周波数フォーマットをダイレクトストリームデジタル(Direct Stream Digital, DSD)という方式と紹介される場合も多い。



しかしこの方式は、スイッチのON/OFFサイクルが分解能に比例して長くなるので、仮に16Bit44.1KHzをこの方式で実現するには、ON時間をサンプリングレートに対し、1~1/65535まで可変させる必要があり、2.89GHzの速度でスイッチを制御しなければなりません。このような速度でON/OFFできるアナログスイッチはありませんし、制御用のワイヤドロジックも2.89GHz以上の速度で動かさねばらならず、1980年代当時は実現困難でしたし、今日でもかなり困難でしょう。そこで⊿Σ変調DACが現れます。
------------------------------------------------------------------------------------------------------------------
ΔΣ変調とはなにか
LPCM [liner palse code modulation]
再度デジタル[LPCM]化を確認したい。前々回のブログの引用で、この様に記している。
”本来電圧値は時間によって変化するので、アナログ的には時間(t)の関数 として捉えますが、デジタル処理では連続したものは扱えませんので、離散的なデータに変換します。これが「標本化」(サンプリング)です。各標本は「 時間の関数」ではなく単純な「量」です。
更にその「量」もまた、もともとはアナログ量(どんな値でもアリ)なんで すが、最大値と最小値を決めて、その間を6万5千段階に区切って、そのどれかのうち最も近い値(最初は単純に端数切り捨てか切り上げでしたが、最近は もうちょっと賢い処理をしています)を選びます。これが量子化(クォンタムノイズ)です。電圧値もまた連続量ではなく、離散的な値になります。
多くの人が混同しているのは、この点で、ネット上の質問欄に同様の質問がされているので、参考にさせて頂きたい。
DAC に於けるΔΣ変調の原理と効能は? http://okwave.jp/qa/q7215315.html
1bitΔΣ型DA変換のノイズシェーピングについて http://oshiete.goo.ne.jp/qa/6772888.html
ΔΣ型1bitDACの有効ビット数について http://oshiete.goo.ne.jp/qa/6707693.html
SACDの可聴高音域での有効ビットについて http://oshiete.goo.ne.jp/qa/6638629.html
ΔΣ変調の疑問のまとめ
多くの人が指摘する代表的な疑問点。
1.CD規格 16ビット 44.1Hz 65535諧調 と 等価である 1ビットコンバーターは1~1/65535まで可変させる必要があり、2.89GHzのサンプリングが必要である筈なのに、実際は64倍~124倍のサンプリング周波数で、これでは、65535諧調の分解能を達成できないのではないか?
2.ΔΣ変調 わざわざ造った規格16ビットを1ビットに変換するメリットは何か?
3.ΔΣ変調は必ずADコンバータの解説となっている。
4.1ビットコンバーターの分解能はどの位あるのか?
質問者の要点を青字で強調してあります。対する回答者の要点を赤字で表記します。
末尾に、これの見解を記載しています。
----------------------------------------------------------------------------------------------------------------------
【DSD】
オーディオ用途で主に用いられるサンプリング周波数はCD-DAの規格である44.1kHzの64倍=2.8224MHz。ダイレクトストリームデジタル (Direct Stream Digital) は、スーパーオーディオCDがアナログ音声をデジタル信号化する際の方式。オーディオの世界においてはCD-DAに用いられるリニアPCM方式に代わる新技術であるが、原理自体は新しいものではなく、古くからあるパルス変調の一つであるPDM方式(パルス密度変調方式)にキャッチーな名前を付けただけである。
更に付け加えれば、CDの上級規格として登場した【SACD】は別の規格であるが、実質の内容はこれもΔΣ変調を採用した高速標本化低bitである。現在、先端とされるデジタル化オーディオはΔΣ変調を基本原理・原則としたTDA-1547のビット・ストリームを嚆矢とするという事のようである。
話が前後するかもしれないが、順番に見ていきたい。しかし、このΔΣ変調というのは、色々調べても、よく解らない。調べれるほどに次なる疑問が出てきて、先週アップする予定が延びてしまった。釈然としない所も在るが、現状での理解という事で、間違っているかもしれないが。
下記サイトに解説されているので、是非読んで頂きたい。
1ビットオーディオの原理と利点は? 後半に全文引用掲載。
みんなDSDを聴いている 概念的にわかりやすいので参考にしてください。
An Introduction to Sigma Delta Converters 英文ですが、詳しいです。
ナチュラルスピード サヤ コンバータの変遷を実証的な解説で、解り良いくお勧め。
----------------------------------------------------------------------------------------------------------------------
1ビットコンバータ
リニアPCMでの製造精度に汲々としたフィリップスは、次なるチャレンジとしたワンビット。デジタルが【0・1】で表現され、出力を【0・1】一つにして、オン・オフを必要回数繰り返してデジタル信号化すれば、製造精度の問題から開放され、オン・オフの回数を上げれば情報量も上げる事が出来ることは、何となく理解できる。
- サヤ殿のホームページより借用 -

オン・オフだけでCD規格16bit、65535通りの振幅を表現するには、信号の周波数の65535x2倍のサンプリング周波数が必要になってしまうが実際はそうなってはいない。このΔΣ変調回路調べてみるとなんとも不思議な考えの上に成立している事が判ってくる。
----------------------------------------------------------------------------------------------------------------------
電流源は1個しかなく、信号の大きさでスイッチのON時間が決まります。ON時間に応じてアンプの出力にはパルス幅変調のかかった電圧が発生しますから、これをローパスフィルタで平均化すれば、DACとして動作します。この方式の最大の長所は、電流源が1個しかないので、マルチビット型で生じる、精度の問題から解消され、優れた直線性を実現できる点にある。下図の黒は上のアンプの出力に発生するパルス幅変調の波形、赤はローパスフィルタ経由した波形です。
オーディオ用途で主に用いられるサンプリング周波数はCD-DAの規格である44.1kHzの64倍=2.8224MHz。ダイレクトストリームデジタル (Direct Stream Digital) は、スーパーオーディオCDがアナログ音声をデジタル信号化する際の方式。オーディオの世界においてはCD-DAに用いられるリニアPCM方式に代わる新技術であるが、原理自体は新しいものではなく、古くからあるパルス変調の一つであるPDM方式(パルス密度変調方式)にキャッチーな名前を付けただけである。
【ΔΣ変調回路】
ワンビットの基礎的な技術は、ウィキペディアによると”1960年代初めに当時学生であった早稲田大学理工学部教授の安田靖彦が開発した”とある。最先端のデジタル技術は、この日本で50年前に考えられた技術を源流としている。
ワンビットの基礎的な技術は、ウィキペディアによると”1960年代初めに当時学生であった早稲田大学理工学部教授の安田靖彦が開発した”とある。最先端のデジタル技術は、この日本で50年前に考えられた技術を源流としている。
----------------------------------------------------------------------------------------------------------------------
このワンビットは、マルチビットと比較して評価では一歩遅れを取っている印象で、コンバータ単体でもマルチビットの方が評価されているようだ。 ところがところが、このワンビットは、現在デジタル化オーディオで一番高音質といわれてDSDと基本原理・原則は同じなのである。更に付け加えれば、CDの上級規格として登場した【SACD】は別の規格であるが、実質の内容はこれもΔΣ変調を採用した高速標本化低bitである。現在、先端とされるデジタル化オーディオはΔΣ変調を基本原理・原則としたTDA-1547のビット・ストリームを嚆矢とするという事のようである。
話が前後するかもしれないが、順番に見ていきたい。しかし、このΔΣ変調というのは、色々調べても、よく解らない。調べれるほどに次なる疑問が出てきて、先週アップする予定が延びてしまった。釈然としない所も在るが、現状での理解という事で、間違っているかもしれないが。
下記サイトに解説されているので、是非読んで頂きたい。
1ビットオーディオの原理と利点は? 後半に全文引用掲載。
みんなDSDを聴いている 概念的にわかりやすいので参考にしてください。
An Introduction to Sigma Delta Converters 英文ですが、詳しいです。
ナチュラルスピード サヤ コンバータの変遷を実証的な解説で、解り良いくお勧め。
----------------------------------------------------------------------------------------------------------------------
1ビットコンバータ
リニアPCMでの製造精度に汲々としたフィリップスは、次なるチャレンジとしたワンビット。デジタルが【0・1】で表現され、出力を【0・1】一つにして、オン・オフを必要回数繰り返してデジタル信号化すれば、製造精度の問題から開放され、オン・オフの回数を上げれば情報量も上げる事が出来ることは、何となく理解できる。
- サヤ殿のホームページより借用 -

オン・オフだけでCD規格16bit、65535通りの振幅を表現するには、信号の周波数の65535x2倍のサンプリング周波数が必要になってしまうが実際はそうなってはいない。このΔΣ変調回路調べてみるとなんとも不思議な考えの上に成立している事が判ってくる。
----------------------------------------------------------------------------------------------------------------------
電流源は1個しかなく、信号の大きさでスイッチのON時間が決まります。ON時間に応じてアンプの出力にはパルス幅変調のかかった電圧が発生しますから、これをローパスフィルタで平均化すれば、DACとして動作します。この方式の最大の長所は、電流源が1個しかないので、マルチビット型で生じる、精度の問題から解消され、優れた直線性を実現できる点にある。下図の黒は上のアンプの出力に発生するパルス幅変調の波形、赤はローパスフィルタ経由した波形です。

しかしこの方式は、スイッチのON/OFFサイクルが分解能に比例して長くなるので、仮に16Bit44.1KHzをこの方式で実現するには、ON時間をサンプリングレートに対し、1~1/65535まで可変させる必要があり、2.89GHzの速度でスイッチを制御しなければなりません。このような速度でON/OFFできるアナログスイッチはありませんし、制御用のワイヤドロジックも2.89GHz以上の速度で動かさねばらならず、1980年代当時は実現困難でしたし、今日でもかなり困難でしょう。そこで⊿Σ変調DACが現れます。
------------------------------------------------------------------------------------------------------------------
ΔΣ変調とはなにか
LPCM [liner palse code modulation]
再度デジタル[LPCM]化を確認したい。前々回のブログの引用で、この様に記している。
”本来電圧値は時間によって変化するので、アナログ的には時間(t)の関数 として捉えますが、デジタル処理では連続したものは扱えませんので、離散的なデータに変換します。これが「標本化」(サンプリング)です。各標本は「 時間の関数」ではなく単純な「量」です。
更にその「量」もまた、もともとはアナログ量(どんな値でもアリ)なんで すが、最大値と最小値を決めて、その間を6万5千段階に区切って、そのどれかのうち最も近い値(最初は単純に端数切り捨てか切り上げでしたが、最近は もうちょっと賢い処理をしています)を選びます。これが量子化(クォンタムノイズ)です。電圧値もまた連続量ではなく、離散的な値になります。
時間軸方向にfsを限りなく上げ、電圧値方向にはbit数を限りなく増やせば「離散」ではありますが「連続」と区別できなくなります。数学で言うと ころの「極限」は「アナログと同じ」です。でも実際には家庭で購入出来る価格でなければ意味がないので、その範囲で限界がありました。その値が44. 1KHzであり16bitだったのです。時間方向には44.1KHz、電圧値方向には16bit。この「細かさ」が「充分」かどうかは当時から議論の的でした。さてお気付きでしょうか。CDに刻まれた信号はそもそも「階段上の波形」なのだという事に。このギザギザが「量子化ノイズ」です。このノイズは凄く 大きなエネルギーを持っていますが、幸いな事に信号(20KHzまで)より高い周波数です。*(シャノンの定理から)そこでフィルタを通して不必要な高い周波数の成分を除去( 波形を滑らかに)してやると、元と変わらぬきれいな波形を再現できます。”
1ビット[⊿Σ変調]
ウィキペディア DSDの説明に、原理はパルス変調の一つ PDM方式(パルス密度変調方式)と書かれている。デジタルといえばコーディングされた二値信号と考えてしまうが、ΔΣ変調でのデジタルは搬送波として使われて、元信号のアナログ信号を連続量として扱いこれで変調している。
つまり、デジタル[LPCM]化では扱えないとしていた連続した時間(t)の関数として捉えている。デジタルという言葉で同じような概念を持ってしまうが、実は、1ビット[⊿Σ変調]はデジタルを符号化に使っている訳ではなくて、パルス変調につまり、搬送波にデジタル矩形はを使っているという事なのである。そのためデジタル演算が出来ないと言う看過できないデメリットがある。
デジタルと言いながら、LPCMとはまったく異なった概念に基づいたモノである。
ΔΣ変調の疑問 1ビット[⊿Σ変調]
ウィキペディア DSDの説明に、原理はパルス変調の一つ PDM方式(パルス密度変調方式)と書かれている。デジタルといえばコーディングされた二値信号と考えてしまうが、ΔΣ変調でのデジタルは搬送波として使われて、元信号のアナログ信号を連続量として扱いこれで変調している。
つまり、デジタル[LPCM]化では扱えないとしていた連続した時間(t)の関数として捉えている。デジタルという言葉で同じような概念を持ってしまうが、実は、1ビット[⊿Σ変調]はデジタルを符号化に使っている訳ではなくて、パルス変調につまり、搬送波にデジタル矩形はを使っているという事なのである。そのためデジタル演算が出来ないと言う看過できないデメリットがある。
デジタルと言いながら、LPCMとはまったく異なった概念に基づいたモノである。
多くの人が混同しているのは、この点で、ネット上の質問欄に同様の質問がされているので、参考にさせて頂きたい。
DAC に於けるΔΣ変調の原理と効能は? http://okwave.jp/qa/q7215315.html
1bitΔΣ型DA変換のノイズシェーピングについて http://oshiete.goo.ne.jp/qa/6772888.html
ΔΣ型1bitDACの有効ビット数について http://oshiete.goo.ne.jp/qa/6707693.html
SACDの可聴高音域での有効ビットについて http://oshiete.goo.ne.jp/qa/6638629.html
ΔΣ変調の疑問のまとめ
多くの人が指摘する代表的な疑問点。
1.CD規格 16ビット 44.1Hz 65535諧調 と 等価である 1ビットコンバーターは1~1/65535まで可変させる必要があり、2.89GHzのサンプリングが必要である筈なのに、実際は64倍~124倍のサンプリング周波数で、これでは、65535諧調の分解能を達成できないのではないか?
2.ΔΣ変調 わざわざ造った規格16ビットを1ビットに変換するメリットは何か?
3.ΔΣ変調は必ずADコンバータの解説となっている。
4.1ビットコンバーターの分解能はどの位あるのか?
質問者の要点を青字で強調してあります。対する回答者の要点を赤字で表記します。
末尾に、これの見解を記載しています。
----------------------------------------------------------------------------------------------------------------------
DAC に於けるΔΣ変調の原理と効能は?
ΔΣ変調の原理と効能は AD 変換に於いては理解できるのですが 0101 の並びに過ぎないことから 0 か 1 かを判断できれば良い筈の Digital Audio 信号をΔΣ変調することは、どのような仕組みになっていてどのような効能があるのでしょうか?
積分器と量子化器との Feedback Loop で構成されるΔΣ変調器の解説はあくまでも Analog 信号を Digitize する際のものであり、DAC (Digital Analog Converter) に於ける Digital to Digital のΔΣ変調には該当しない筈だと思うのですが違うのでしょうか?
もしも AD 変換時のΔΣ変調器と同様の回路が DAC に組み込まれているのであれば 0101 の Digital Code を判断するのに何故そのような Analog 検波機構が必要なのか理解できません。
また Analog 検波に於いては 22.05kHz 16bit (65536 階調) の電圧変化全てを正確に 1bit へ量子化するためには 44.1kHz × 65536 の 65536 倍 Over Sampling を要すると思うのですが、128 倍などと低 Over Sampling 値で Digitize する現在のΔΣ変調型 ADC では何故初期の Single Bit DAC (PHILIPS SA7221 や PANASONIC MASH など) にみられた「大音量の高域ほど Data が欠落したような Mellow な音質になる」という問題が起きないのかも不思議です。
DAC に於いては 0101 の Code を正確に読み取りさえすれば正確な波形を再現することに何の支障もない筈で、Over Sampling は高額の開発費がかかるにもかかわらず音質劣化の主原因となる多素子 LPF (Low Pass Filter) の使用を避ける、SACD/DSD (Super Audio Compact Disc / Direct Stream Digital) に於いては Speaker System の追従限界を超える 高周波の Pulse 発振によって LPF そのものまで不要とするためのものでしかないとさえ思うのですが違うのでしょうか?
正確な正弦波 Pulse を発振させるために Quantum Bit 数を増やすこととなる Digital to Digital の Over Sampling は Quantum Noise の発生が止むを得ないものですが、この Noise を可聴帯域外に Shift する Noise Shaping にしても Digital Computing 演算処理 Algorithm が行うことであって、16 進法と 2 進法といった異なる量子化 Code の比較を行えるわけではない量子化器と積分器の Feedback Loop で解説されるものではないのではと思っているのですが違うのでしょうか?
何故 Analog ではない 0101 の Digital PCM (Pulse Code Modulation) Code を正確に受け取って Pulse 発振すれば良いだけの筈の DAC に於いてもΔΣ変調器が有効なのか、その動作原理と効用について解説をいただき、晴れ々々とした気分で新年を迎えたいのですが(滝汗)・・・宜しく御願いします。
----------------------------------------------------------------------------------------------------------------------
ΔΣ変調をDA変換に使う利点は、そうでないとビットの深い変換が技術的に困難だからだという所も大きいと思います。純粋なマルチビットでビット数を深く取るには非常に高精度な分圧回路が必要です。単純計算で深さが16ビットの場合1ビットはフルスケールの0.0015%、24ビットでは0.000006%となりますから、24ビットの分圧回路など実現不可能なのではないでしょうか。
分圧回路はアナログ技術ですが、ΔΣ変調ではビットストリームを作るまでデジタル処理するので、アナログは最後の積分だけです。ビットストリームの一つ一つのパルスの積分値さえ揃っていれば良い訳ですから、積分器の電源とクロックが安定ならば、クロック周波数を上げて行くだけで分解能を上げて行くことができます。
オーバーサンプリングが何故128倍程度で済んでしまうのか、という点に関しては、私も不思議で、恐らくこれこそがΔΣ型D/A変換の鍵です。ビットストリームを作る時にフィードバックが働いていることが理解を難しくしています。128倍オーバーサンプリングのパルス密度変調を一周期の単位で考えてしまうと22.05kHzの正弦波を65536階調で表現するのは不可能です。しかしΔΣ変調ではフィードバックが働いているためにビットストリームはこの一周期の情報だけでは確定せず、過去の履歴に依存して決まります。このため22.05kHzの正弦波の各々の波が毎回同じでは無いことになります。誤差を22.05kHzの正弦波の揺らぎとして低周波で散らす結果になっていると考えても良いのではないかと思います。この件は私も此処で何度か質問させて頂いているので、よろしかったら御参考までに私の質問を覗いてみてください。
1bitΔΣ型DA変換のノイズシェーピングについて http://oshiete.goo.ne.jp/qa/6772888.html
ΔΣ型1bitDACの有効ビット数について http://oshiete.goo.ne.jp/qa/6707693.html
SACDの可聴高音域での有効ビットについて http://oshiete.goo.ne.jp/qa/6638629.html
----------------------------------------------------------------------------------------------------------------------
1ビットオーディオの原理と利点は? 全文を読んで頂きたい。
ΔΣ変調の原理と効能は AD 変換に於いては理解できるのですが 0101 の並びに過ぎないことから 0 か 1 かを判断できれば良い筈の Digital Audio 信号をΔΣ変調することは、どのような仕組みになっていてどのような効能があるのでしょうか?
積分器と量子化器との Feedback Loop で構成されるΔΣ変調器の解説はあくまでも Analog 信号を Digitize する際のものであり、DAC (Digital Analog Converter) に於ける Digital to Digital のΔΣ変調には該当しない筈だと思うのですが違うのでしょうか?
もしも AD 変換時のΔΣ変調器と同様の回路が DAC に組み込まれているのであれば 0101 の Digital Code を判断するのに何故そのような Analog 検波機構が必要なのか理解できません。
また Analog 検波に於いては 22.05kHz 16bit (65536 階調) の電圧変化全てを正確に 1bit へ量子化するためには 44.1kHz × 65536 の 65536 倍 Over Sampling を要すると思うのですが、128 倍などと低 Over Sampling 値で Digitize する現在のΔΣ変調型 ADC では何故初期の Single Bit DAC (PHILIPS SA7221 や PANASONIC MASH など) にみられた「大音量の高域ほど Data が欠落したような Mellow な音質になる」という問題が起きないのかも不思議です。
DAC に於いては 0101 の Code を正確に読み取りさえすれば正確な波形を再現することに何の支障もない筈で、Over Sampling は高額の開発費がかかるにもかかわらず音質劣化の主原因となる多素子 LPF (Low Pass Filter) の使用を避ける、SACD/DSD (Super Audio Compact Disc / Direct Stream Digital) に於いては Speaker System の追従限界を超える 高周波の Pulse 発振によって LPF そのものまで不要とするためのものでしかないとさえ思うのですが違うのでしょうか?
正確な正弦波 Pulse を発振させるために Quantum Bit 数を増やすこととなる Digital to Digital の Over Sampling は Quantum Noise の発生が止むを得ないものですが、この Noise を可聴帯域外に Shift する Noise Shaping にしても Digital Computing 演算処理 Algorithm が行うことであって、16 進法と 2 進法といった異なる量子化 Code の比較を行えるわけではない量子化器と積分器の Feedback Loop で解説されるものではないのではと思っているのですが違うのでしょうか?
何故 Analog ではない 0101 の Digital PCM (Pulse Code Modulation) Code を正確に受け取って Pulse 発振すれば良いだけの筈の DAC に於いてもΔΣ変調器が有効なのか、その動作原理と効用について解説をいただき、晴れ々々とした気分で新年を迎えたいのですが(滝汗)・・・宜しく御願いします。
----------------------------------------------------------------------------------------------------------------------
ΔΣ変調をDA変換に使う利点は、そうでないとビットの深い変換が技術的に困難だからだという所も大きいと思います。純粋なマルチビットでビット数を深く取るには非常に高精度な分圧回路が必要です。単純計算で深さが16ビットの場合1ビットはフルスケールの0.0015%、24ビットでは0.000006%となりますから、24ビットの分圧回路など実現不可能なのではないでしょうか。
分圧回路はアナログ技術ですが、ΔΣ変調ではビットストリームを作るまでデジタル処理するので、アナログは最後の積分だけです。ビットストリームの一つ一つのパルスの積分値さえ揃っていれば良い訳ですから、積分器の電源とクロックが安定ならば、クロック周波数を上げて行くだけで分解能を上げて行くことができます。
オーバーサンプリングが何故128倍程度で済んでしまうのか、という点に関しては、私も不思議で、恐らくこれこそがΔΣ型D/A変換の鍵です。ビットストリームを作る時にフィードバックが働いていることが理解を難しくしています。128倍オーバーサンプリングのパルス密度変調を一周期の単位で考えてしまうと22.05kHzの正弦波を65536階調で表現するのは不可能です。しかしΔΣ変調ではフィードバックが働いているためにビットストリームはこの一周期の情報だけでは確定せず、過去の履歴に依存して決まります。このため22.05kHzの正弦波の各々の波が毎回同じでは無いことになります。誤差を22.05kHzの正弦波の揺らぎとして低周波で散らす結果になっていると考えても良いのではないかと思います。この件は私も此処で何度か質問させて頂いているので、よろしかったら御参考までに私の質問を覗いてみてください。
1bitΔΣ型DA変換のノイズシェーピングについて http://oshiete.goo.ne.jp/qa/6772888.html
ΔΣ型1bitDACの有効ビット数について http://oshiete.goo.ne.jp/qa/6707693.html
SACDの可聴高音域での有効ビットについて http://oshiete.goo.ne.jp/qa/6638629.html
----------------------------------------------------------------------------------------------------------------------
1ビットオーディオの原理と利点は? 全文を読んで頂きたい。
質問
ちょっと前から1ビットオーディオが流行っているようですが、いまいち原理が理解できません。
・これは、CDのPCMが16bit44.1kHzであるように1bit11.2MHzのPCMだと考えてよいのでしょうか?
言い方を変えれば、300dpi256色のグラデーションと4800dpiの白黒ディザリングの違いのように理解していますがそれで正しいのでしょうか?
・増幅時にDA変換を通さないので音が良いと聞きますが、1bitなのにどうやって変換するのでしょうか?highとlowの値自体を変化させるのでしょうか?
また、従来でも16ビットまたはそれ以上のデジタル変換はあったと思うのですがそれと比べてなぜ音が良いのでしょうか?
・「ΔΣ変調」というものがあって、原理図を見るとFM変調を矩形波でやっているように見えますがそれであっていますか?
・ローパスフィルタでΔΣ変調されたデータが元波形になる理屈を教えてください。
また、そのときに音質が劣化するのではないでしょうか?
・素直にPCMの量子化ビット数を上げていればいいのではないですか?何か1bitならではの利点があるのですか?
----------------------------------------------------------------------------------------------------------------------
回答
1.>>ΔΣ変調の原理は周波数変調を矩形波でやっているように見えますがそれであっていますか? <<
いい眼力です! そう見抜けた人には「ΔΣ方式の何が優れてるのか」が丸見えなのです。 FM と同じようにノイズ(変換誤差)の周波数特性が三角形だからです。
「増幅時にDA変換を通さないので音が良いと聞きますが」と言いますが実際は1bitのDA変換です。1bitなわけは、ΔΣ方式が(オーディオ帯では)1bitで十分だからです。でも1bitであることとΔΣ方式が優れてることとは関係ありませんので。
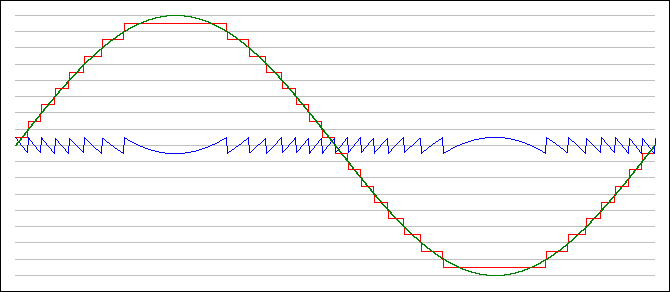
基本の PCM 波形です。
http://www.beis.de/Elektronik/DeltaSigma/ADCSinu …
黒…原波形
赤…PCMの復号波
青…いわゆる量子化ノイズです。
これを手掛かりに、ディジタル変調をこんなふうに捉えてください;
原波形に 方式固有のノイズ を加えたものが復調波形である。と。
----------------------------------------------------------------------------------------------------------------------
PCMの方式ノイズは広く知られてる「電圧コンパレータの階段のギザギザ」ってやつです。これには周波数特性などありませんから 量子化ノイズの振幅も周波数特性はありません、下図で横一直線です。
2.
FM はAMと同じ純アナログなので変調誤差的ノイズは存在しません。伝送途中で加わる外来ノイズを考えます。復調の方は周波数を振幅に変える回路を使います。昔はフィルタの傾斜部分、現在はPLLですね。
FM波 ──C─┬─ 復調波出力
|
R (実際は LC 同調回路の
| 同調付近の急勾配を使う)
┷
PLLの場合 ここに
復調波が出る
|
FM波 ─減算───ローパス─┴─可変──┐
(位相比較) フィルタ 発振器 |
└──────────────┘
復調出力の振幅
| ____
| /
| /上図のどちらも
| / ハイパスフィルタの
| / 傾斜部分を利用しています
|
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄周波数
伝送途中で加わるノイズもハイパスフィルタを通ります。普通のノイズは周波数分布が一様なので、ハイパスフィルタを通った後は 右上がりの三角形になります。実は、これはノイスシェーピングそのものの働きです。
↓ナマのFM放送電波では搬送波を中心に左右対称になってます。
http://www.vk1od.net/FM/fmtri.gif
これを復調すると 左半分が右に折り重なります。

3.PCMとFMのノイズの周波数特性;
ノイズの振幅
|
| FMのノイズ
| / (三角状)
| _/
| ̄/ ̄ ̄ ̄普通のPCMのノイズ
|/ (一様)
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄周波数
もしΔΣ変調のノイズも三角形ならば、図の原点に近い所ほどPCMより勝ってますね。 たったこれだけです、この範囲で動作するようにすれば、ΔΣ方式は PCM 方式よりも SN比を良くできる、ということです。
なお、解説記事でよくある「1bitだから階段状電圧ステップの不揃いが関係しない…」という話は1bit構成にした場合だけの話で、上記の長所には bit数は無関係です。
( 多bit構成も行われてますし、振幅が量子力学的に量子化される超伝導回路での開発が盛んです。)
4.ΔΣ変調回路
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
この変換誤差(方式ノイズ)が三角ノイズになる仕組みを説明します。
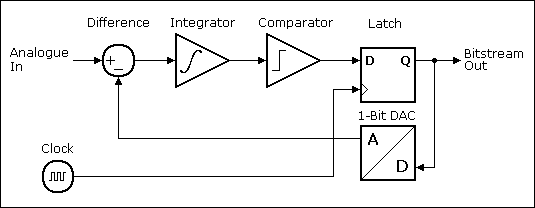
まず↓量子化ノイズの波形(青色)。
http://www.beis.de/Elektronik/DeltaSigma/ADCSinu …
事前に何か適当な回路で、これそっくりな波形を作ったと仮定します。
その波形を使って『原波形に方式固有ノイズを加えたものが復調波形である。』
を、
↓この定番モデルで説明します。
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
↑オペアンプで作った普通のアナログ回路だと考えてください、
こんな。↓
量子化ノイズと
┌─ C ─┐| 同じ波形を
| || 外部から加える
原信号─R┬┴|-\ |└R┐
┌R┘ |-A >-┴─R┼─ ΔΣ変調パルス
| ┌|+/ |
| ┷ |
└────←適当に─┘
バッファアンプが
あると思ってください
量子化ノイズのそっくりさんを足されたあとの波形は、コンパレータの出力パルスとそっくりな形になることを理解してください。←ここが肝です。
図はめんどいので文字化します。↓
量子化ノイズと
そっくりな波形─┐
|
原信号 ─減算──積分回路 ─ 加算─┬─ ΔΣ変調パルス
| |
└──────── ───┘
量子化ノイズ波形のみの周波数特性が見えやすくするため、原信号入力=ゼロとすると、
量子化ノイズと
そっくりな波形─┐
|
┌─反転入力──積分回路 ─ 加算─┬─ ΔΣ変調パルス
| |
└──────────────---┘
↓回路変えずに場所だけ移動します。
量子化ノイズと
そっくりな波形 ┌ ΔΣ変調パルス
| |
└─加算─┴─反転入力積分回路─┐
| |
└──────── ────┘
前記のPLLとそっくりな構成になりましたね、オペアンプで書けば、
量子化ノイズと ΔΣ変調パルス出力
そっくりな波形 ↑
↓ | ┌─ C ─┐
| | | |
└─R┬─バッファ ─┴─R ┴|-\ |
┌─R┘ アンプ | -A >─┤
| ┌|+/ |
| ┷ |
└────────────────┘
図の右半分は ただの積分回路ですから 出力を式で書くと
(出力) = (量子化ノイズ入力)-(出力を積分した波形)
ですね、
引き算になるわけは積分回路で正負反転するからです。
周波数で書くと積分は 1/jω を掛けることだから、
(出力) = (量子化ノイズ入力)-(出力)/jω
jω(出力) = jω(量子化ノイズ入力)-(出力)
(出力)(1+jω) = jω(量子化ノイズ入力)
∴
(出力)/(入力) = jω/(1+jω) = ハイパスフィルタそのもの
です。
すなわち、FMと同じく量子化ノイズは 右上がりの三角形になるのでした。よって、3項の図の原点付近で動作するようにすれば、PCMよりも方式ノイズを減らせる、ということです。
これが一応、原理の基本部分です。
----------------------------------------------------------------------------------------------------------------------
まとめると;
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …

出力の瞬時値は「普通のPCMの量子化ノイズ」と同じ振幅です。しかし積分器の出力ではその周波数成分が低域ほど落ちてます。その事を上記で延々と説明しました。
で、復号する側は この積分器とそっくりな回路ですから その出力も(量子化ノイズ成分に関して)まったく同じ周波数特性なわけです。
5.さらなる工夫。
http://www.apec.aichi-c.ed.jp/shoko/kyouka/math/ …
↑原点付近では、紫の直線 y=x よりも y=x^2 の方が下に居ます。さらに y=x^3, y=x^4 ならもっと下になりますね、つまり積分を何重にもすればするほど量子化ノイズを小さくできるわけです。これがPCMをしのいでΔΣぶっちぎりになった肝です。
↓二重積分の構成
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
さらに、
普通 PCM は、サンプリング周波数の半分の帯域に 入力を制限しないと エリアシングが発生します。これはアナログ段階でやらないといけないですが、スパッと垂直に切れるアナログフィルタは難しく、妥協して作らざるを得ず、信号が少し削られたり形がいびつになったりします。そこで、オーバーサンプリングと称して、サンプリング周波数を必要以上に思い切り高くして信号帯域との間を広くとって、フィルタを作りやすくします。
↓普通のADコンバータとΔΣコンバータの比較。
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
黄色いゾーンが距離かせぎです。
1bit構成が好まれる理由は回路的に単純で高速にできるからです。この辺は古典的電子回路と量子力学的電子回路で話が分かれますが省略します。
得られた1bitのデータ列は まさにFMそのものです。PNMとかPDMとも称します。これ以降はディジタルフィルタの話になります。 SN比改善の具体的なことは 積分の次数と オーバーサンプリングの倍数で決まりますが、ディジタルフィルタの説明までは書き切れませんので省略させてください。 ΔΣ方式の肝は 積分で量子化ノイズが三角形になる所です。
6.>> ・ローパスフィルタでΔΣ変調されたデータが元波形になる理屈を教えてください。 <<
4項の最後に書いた「まとめ」そのままです;
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
↑出力の瞬時値は「普通のPCMの量子化ノイズ」と同じ振幅です。しかし積分器の出力ではその周波数成分が低域ほど落ちてます。その事を4項で延々と説明しました。
で、復号する側は この積分器とそっくりな回路があるだけですから その出力も(量子化ノイズ成分に関して)まったく同じ周波数特性なわけです。
このことはDAのbit数には関係ありません、1bitDAでも多bitDAでも同じです。
あなたが「周波数変調を矩形波でやっているように見えます」とお書になった矩形波をローパスフィルタに入れて、矩形波成分を阻止して信号成分だけを通過させてるだけです。普通のローパスの機能そのままです。
7.>> いまいち原理が理解できません。 <<
こんなに広まってるのに「発明者に聞く」みたいな記事に出会ったことがありますか? 実は ΔΣ変換は 日本で生まれたんですが御存知でした?
http://www.soumu.go.jp/iicp/chousakenkyu/data/re …
地味な前世紀中葉の日本昔話は化石なのでしょうか、国外の文献では発明者の名前を散見しますが日本では知名度ゼロでしょう。 これも八木アンテナのように伝説の殿堂入りですね。 上記サイトを紹介しようと書き始めたら長くなってしまいした、この辺で。( 分かり易くするために不正確なところもあります、かなり昔のやつのツギハギなので変なところは御容赦を。)
---------------------------------------------------------------------------------------------------------------------ΔΣ変調の疑問への見解
1.CD規格 16ビット 44.1Hz 65535諧調 と 等価である 1ビットコンバーターは1~1/65535まで可変させる必要があり、2.89GHzのサンプリングが必要である筈なのに、実際は64倍~124倍のサンプリング周波数で、これでは、65535諧調の分解能を達成できないのではないか?
前述に”量子化ノイズは 右上がりの三角形になる”とあるが、量子化ノイズが三角波になるためにフーリエ変換すると、無限にフーリエ変換する必要はなく100倍(2のべき数から64倍か124倍)あれば、充分に三角波と見なせる。高周波の飛付きを避ける為にもサンプリング周波数は出来るだけ低く抑えるため、64倍~124倍が選ばれている。
2.ΔΣ変調 わざわざ造った規格16ビットを1ビットに変換するメリットは何か?
・生産技術に大きな負担となる精度の問題から開放される。
ちょっと前から1ビットオーディオが流行っているようですが、いまいち原理が理解できません。
・これは、CDのPCMが16bit44.1kHzであるように1bit11.2MHzのPCMだと考えてよいのでしょうか?
言い方を変えれば、300dpi256色のグラデーションと4800dpiの白黒ディザリングの違いのように理解していますがそれで正しいのでしょうか?
・増幅時にDA変換を通さないので音が良いと聞きますが、1bitなのにどうやって変換するのでしょうか?highとlowの値自体を変化させるのでしょうか?
また、従来でも16ビットまたはそれ以上のデジタル変換はあったと思うのですがそれと比べてなぜ音が良いのでしょうか?
・「ΔΣ変調」というものがあって、原理図を見るとFM変調を矩形波でやっているように見えますがそれであっていますか?
・ローパスフィルタでΔΣ変調されたデータが元波形になる理屈を教えてください。
また、そのときに音質が劣化するのではないでしょうか?
・素直にPCMの量子化ビット数を上げていればいいのではないですか?何か1bitならではの利点があるのですか?
----------------------------------------------------------------------------------------------------------------------
回答
1.>>ΔΣ変調の原理は周波数変調を矩形波でやっているように見えますがそれであっていますか? <<
いい眼力です! そう見抜けた人には「ΔΣ方式の何が優れてるのか」が丸見えなのです。 FM と同じようにノイズ(変換誤差)の周波数特性が三角形だからです。
「増幅時にDA変換を通さないので音が良いと聞きますが」と言いますが実際は1bitのDA変換です。1bitなわけは、ΔΣ方式が(オーディオ帯では)1bitで十分だからです。でも1bitであることとΔΣ方式が優れてることとは関係ありませんので。
基本の PCM 波形です。
http://www.beis.de/Elektronik/DeltaSigma/ADCSinu …
黒…原波形
赤…PCMの復号波
青…いわゆる量子化ノイズです。
これを手掛かりに、ディジタル変調をこんなふうに捉えてください;
原波形に 方式固有のノイズ を加えたものが復調波形である。と。
----------------------------------------------------------------------------------------------------------------------
PCMの方式ノイズは広く知られてる「電圧コンパレータの階段のギザギザ」ってやつです。これには周波数特性などありませんから 量子化ノイズの振幅も周波数特性はありません、下図で横一直線です。
量子化ノイズの振幅
|
|
|
|_____横一直線
|
|
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄周波数
FM はAMと同じ純アナログなので変調誤差的ノイズは存在しません。伝送途中で加わる外来ノイズを考えます。復調の方は周波数を振幅に変える回路を使います。昔はフィルタの傾斜部分、現在はPLLですね。
FM波 ──C─┬─ 復調波出力
|
R (実際は LC 同調回路の
| 同調付近の急勾配を使う)
┷
PLLの場合 ここに
復調波が出る
|
FM波 ─減算───ローパス─┴─可変──┐
(位相比較) フィルタ 発振器 |
└──────────────┘
復調出力の振幅
| ____
| /
| /上図のどちらも
| / ハイパスフィルタの
| / 傾斜部分を利用しています
|
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄周波数
伝送途中で加わるノイズもハイパスフィルタを通ります。普通のノイズは周波数分布が一様なので、ハイパスフィルタを通った後は 右上がりの三角形になります。実は、これはノイスシェーピングそのものの働きです。
↓ナマのFM放送電波では搬送波を中心に左右対称になってます。
http://www.vk1od.net/FM/fmtri.gif
これを復調すると 左半分が右に折り重なります。

3.PCMとFMのノイズの周波数特性;
ノイズの振幅
|
| FMのノイズ
| / (三角状)
| _/
| ̄/ ̄ ̄ ̄普通のPCMのノイズ
|/ (一様)
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄周波数
もしΔΣ変調のノイズも三角形ならば、図の原点に近い所ほどPCMより勝ってますね。 たったこれだけです、この範囲で動作するようにすれば、ΔΣ方式は PCM 方式よりも SN比を良くできる、ということです。
なお、解説記事でよくある「1bitだから階段状電圧ステップの不揃いが関係しない…」という話は1bit構成にした場合だけの話で、上記の長所には bit数は無関係です。
( 多bit構成も行われてますし、振幅が量子力学的に量子化される超伝導回路での開発が盛んです。)
4.ΔΣ変調回路
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
この変換誤差(方式ノイズ)が三角ノイズになる仕組みを説明します。
まず↓量子化ノイズの波形(青色)。
http://www.beis.de/Elektronik/DeltaSigma/ADCSinu …
事前に何か適当な回路で、これそっくりな波形を作ったと仮定します。
その波形を使って『原波形に方式固有ノイズを加えたものが復調波形である。』
を、
↓この定番モデルで説明します。
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
↑オペアンプで作った普通のアナログ回路だと考えてください、
こんな。↓
量子化ノイズと
┌─ C ─┐| 同じ波形を
| || 外部から加える
原信号─R┬┴|-\ |└R┐
┌R┘ |-A >-┴─R┼─ ΔΣ変調パルス
| ┌|+/ |
| ┷ |
└────←適当に─┘
バッファアンプが
あると思ってください
量子化ノイズのそっくりさんを足されたあとの波形は、コンパレータの出力パルスとそっくりな形になることを理解してください。←ここが肝です。
図はめんどいので文字化します。↓
量子化ノイズと
そっくりな波形─┐
|
原信号 ─減算──積分回路 ─ 加算─┬─ ΔΣ変調パルス
| |
└──────── ───┘
量子化ノイズ波形のみの周波数特性が見えやすくするため、原信号入力=ゼロとすると、
量子化ノイズと
そっくりな波形─┐
|
┌─反転入力──積分回路 ─ 加算─┬─ ΔΣ変調パルス
| |
└──────────────---┘
↓回路変えずに場所だけ移動します。
量子化ノイズと
そっくりな波形 ┌ ΔΣ変調パルス
| |
└─加算─┴─反転入力積分回路─┐
| |
└──────── ────┘
前記のPLLとそっくりな構成になりましたね、オペアンプで書けば、
量子化ノイズと ΔΣ変調パルス出力
そっくりな波形 ↑
↓ | ┌─ C ─┐
| | | |
└─R┬─バッファ ─┴─R ┴|-\ |
┌─R┘ アンプ | -A >─┤
| ┌|+/ |
| ┷ |
└────────────────┘
図の右半分は ただの積分回路ですから 出力を式で書くと
(出力) = (量子化ノイズ入力)-(出力を積分した波形)
ですね、
引き算になるわけは積分回路で正負反転するからです。
周波数で書くと積分は 1/jω を掛けることだから、
(出力) = (量子化ノイズ入力)-(出力)/jω
jω(出力) = jω(量子化ノイズ入力)-(出力)
(出力)(1+jω) = jω(量子化ノイズ入力)
∴
(出力)/(入力) = jω/(1+jω) = ハイパスフィルタそのもの
です。
すなわち、FMと同じく量子化ノイズは 右上がりの三角形になるのでした。よって、3項の図の原点付近で動作するようにすれば、PCMよりも方式ノイズを減らせる、ということです。
これが一応、原理の基本部分です。
----------------------------------------------------------------------------------------------------------------------
まとめると;
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
出力の瞬時値は「普通のPCMの量子化ノイズ」と同じ振幅です。しかし積分器の出力ではその周波数成分が低域ほど落ちてます。その事を上記で延々と説明しました。
で、復号する側は この積分器とそっくりな回路ですから その出力も(量子化ノイズ成分に関して)まったく同じ周波数特性なわけです。
5.さらなる工夫。
http://www.apec.aichi-c.ed.jp/shoko/kyouka/math/ …
↑原点付近では、紫の直線 y=x よりも y=x^2 の方が下に居ます。さらに y=x^3, y=x^4 ならもっと下になりますね、つまり積分を何重にもすればするほど量子化ノイズを小さくできるわけです。これがPCMをしのいでΔΣぶっちぎりになった肝です。
↓二重積分の構成
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
さらに、
普通 PCM は、サンプリング周波数の半分の帯域に 入力を制限しないと エリアシングが発生します。これはアナログ段階でやらないといけないですが、スパッと垂直に切れるアナログフィルタは難しく、妥協して作らざるを得ず、信号が少し削られたり形がいびつになったりします。そこで、オーバーサンプリングと称して、サンプリング周波数を必要以上に思い切り高くして信号帯域との間を広くとって、フィルタを作りやすくします。
↓普通のADコンバータとΔΣコンバータの比較。
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
黄色いゾーンが距離かせぎです。
1bit構成が好まれる理由は回路的に単純で高速にできるからです。この辺は古典的電子回路と量子力学的電子回路で話が分かれますが省略します。
得られた1bitのデータ列は まさにFMそのものです。PNMとかPDMとも称します。これ以降はディジタルフィルタの話になります。 SN比改善の具体的なことは 積分の次数と オーバーサンプリングの倍数で決まりますが、ディジタルフィルタの説明までは書き切れませんので省略させてください。 ΔΣ方式の肝は 積分で量子化ノイズが三角形になる所です。
6.>> ・ローパスフィルタでΔΣ変調されたデータが元波形になる理屈を教えてください。 <<
4項の最後に書いた「まとめ」そのままです;
http://www.beis.de/Elektronik/DeltaSigma/DeltaSi …
↑出力の瞬時値は「普通のPCMの量子化ノイズ」と同じ振幅です。しかし積分器の出力ではその周波数成分が低域ほど落ちてます。その事を4項で延々と説明しました。
で、復号する側は この積分器とそっくりな回路があるだけですから その出力も(量子化ノイズ成分に関して)まったく同じ周波数特性なわけです。
このことはDAのbit数には関係ありません、1bitDAでも多bitDAでも同じです。
あなたが「周波数変調を矩形波でやっているように見えます」とお書になった矩形波をローパスフィルタに入れて、矩形波成分を阻止して信号成分だけを通過させてるだけです。普通のローパスの機能そのままです。
7.>> いまいち原理が理解できません。 <<
こんなに広まってるのに「発明者に聞く」みたいな記事に出会ったことがありますか? 実は ΔΣ変換は 日本で生まれたんですが御存知でした?
http://www.soumu.go.jp/iicp/chousakenkyu/data/re …
地味な前世紀中葉の日本昔話は化石なのでしょうか、国外の文献では発明者の名前を散見しますが日本では知名度ゼロでしょう。 これも八木アンテナのように伝説の殿堂入りですね。 上記サイトを紹介しようと書き始めたら長くなってしまいした、この辺で。( 分かり易くするために不正確なところもあります、かなり昔のやつのツギハギなので変なところは御容赦を。)
---------------------------------------------------------------------------------------------------------------------ΔΣ変調の疑問への見解
1.CD規格 16ビット 44.1Hz 65535諧調 と 等価である 1ビットコンバーターは1~1/65535まで可変させる必要があり、2.89GHzのサンプリングが必要である筈なのに、実際は64倍~124倍のサンプリング周波数で、これでは、65535諧調の分解能を達成できないのではないか?
前述に”量子化ノイズは 右上がりの三角形になる”とあるが、量子化ノイズが三角波になるためにフーリエ変換すると、無限にフーリエ変換する必要はなく100倍(2のべき数から64倍か124倍)あれば、充分に三角波と見なせる。高周波の飛付きを避ける為にもサンプリング周波数は出来るだけ低く抑えるため、64倍~124倍が選ばれている。
2.ΔΣ変調 わざわざ造った規格16ビットを1ビットに変換するメリットは何か?
・生産技術に大きな負担となる精度の問題から開放される。
LPCMでは、ビットの深い変換が技術的に困難で。純粋なマルチビットでビット数を深く取るには非常に高精度な分圧回路が必要となる。単純計算で深さが16ビットの場合1ビットはフルスケールの0.0015%、24ビットでは0.000006%となる。
・必須のフィルターを低次 に出来る。
・デメリットとしてデジタル演算が出来ない。
・必須のフィルターを低次 に出来る。
・デメリットとしてデジタル演算が出来ない。
3.ΔΣ変調は必ずADコンバータの解説となっている。

ADコンバータの模式図を再掲する。Bitstream Out の分岐が1-bit DACとなっており実質はADAコンバータの構成となる。どちらから見るかという視点による。
4.1ビットコンバーターの分解能はどの位あるのか?
デジタルを近似的にアナログ量としているので、分解能はS/N比として捉え、LPCMの分解能では量れない。
--------------------------------------------------------------------------------------------------------------------
⊿Σ変調のメリット サヤ殿から引用
⊿Σ変調の本質は、1Bitではありません。⊿Σ変調の目的をまとめると次の通りになります。
① 入力のデジタル信号のビット数よりも、低ビットDACを、オーバーサンプリングで動かす。
② 低ビットDACで生じた、再量子化ノイズを時間軸で分散、必要(可聴)帯域より高域にシフト。
③ 前記、再量子化ノイズはDACのバックエンドのローパスフィルタで除去する。
④ これらにより必要(可聴)帯域では、低ビットDACの分解能を超えるダイナミックレンジを得る。
実はこのコンセプトのDAC、CDプレーヤーは、CD商品化当初からあったのです。フィリップス/マランツのLHH2000です。このDACは4倍オーバーサンプリング、ノイズシェーパに14BitのマルチビットDACを組み合わせ、16Bitに迫る性能を達成していました。そして当時の他社の16BitDACより優れた性能を達成したと思われます。既に4倍オーバーサンプリング化を達成しているので、バックエンドのローパスフィルタも軽く、優れた位相特性も音質面で有利です。
----------------------------------------------------------------------------------------------------------------------
またしても、LHH2000である。
ADコンバータの模式図を再掲する。Bitstream Out の分岐が1-bit DACとなっており実質はADAコンバータの構成となる。どちらから見るかという視点による。
4.1ビットコンバーターの分解能はどの位あるのか?
デジタルを近似的にアナログ量としているので、分解能はS/N比として捉え、LPCMの分解能では量れない。
--------------------------------------------------------------------------------------------------------------------
⊿Σ変調のメリット サヤ殿から引用
⊿Σ変調の本質は、1Bitではありません。⊿Σ変調の目的をまとめると次の通りになります。
① 入力のデジタル信号のビット数よりも、低ビットDACを、オーバーサンプリングで動かす。
② 低ビットDACで生じた、再量子化ノイズを時間軸で分散、必要(可聴)帯域より高域にシフト。
③ 前記、再量子化ノイズはDACのバックエンドのローパスフィルタで除去する。
④ これらにより必要(可聴)帯域では、低ビットDACの分解能を超えるダイナミックレンジを得る。
実はこのコンセプトのDAC、CDプレーヤーは、CD商品化当初からあったのです。フィリップス/マランツのLHH2000です。このDACは4倍オーバーサンプリング、ノイズシェーパに14BitのマルチビットDACを組み合わせ、16Bitに迫る性能を達成していました。そして当時の他社の16BitDACより優れた性能を達成したと思われます。既に4倍オーバーサンプリング化を達成しているので、バックエンドのローパスフィルタも軽く、優れた位相特性も音質面で有利です。
----------------------------------------------------------------------------------------------------------------------
またしても、LHH2000である。
0 件のコメント:
コメントを投稿